在图像的变换上,我们可以依靠矩阵实现一些基本的线性变换。如scale(缩放)、Reflection(翻转)、Shear(切变)、Rotate(旋转)
2D变换
如下:将图像化为坐标x,y;则可以用矩阵运算表示:
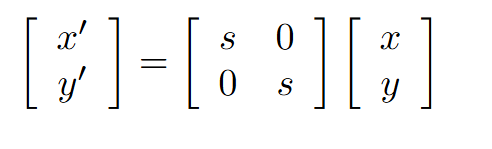
对于图像变换我们一般线性变换都是以公式表示
X` = a x+by ; Y` =c x+ d y;
用矩阵格式则是以下
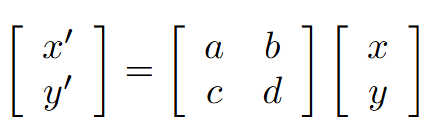
依此,推出其他线性变换的矩阵(基本变换)如下:
基本线性变换:
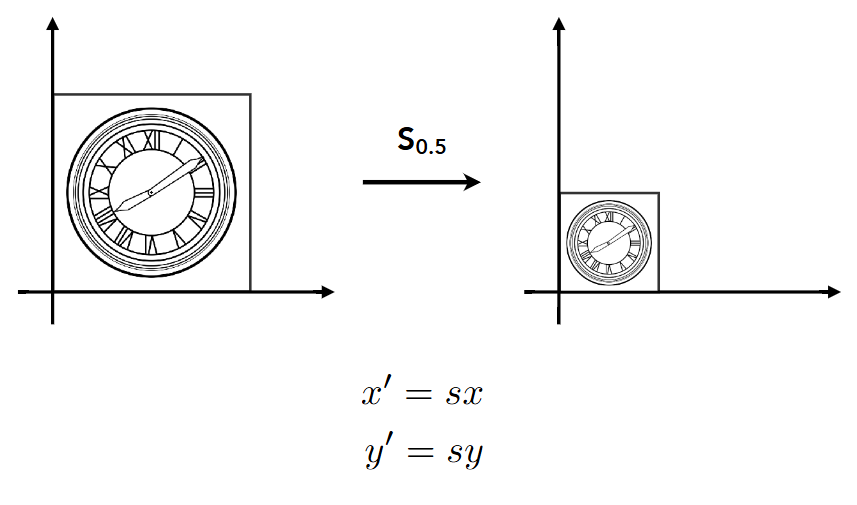
1.1缩放
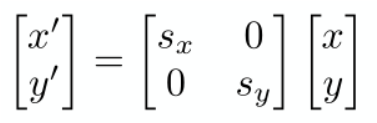
1.2.镜像
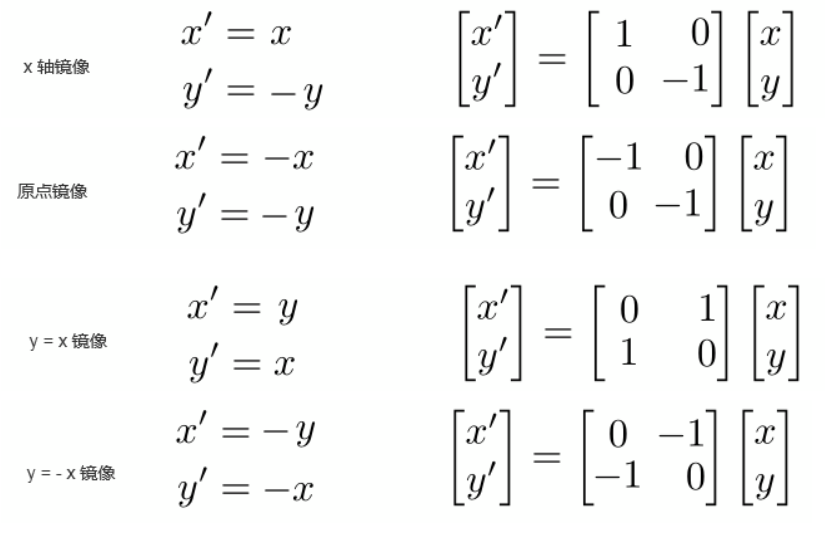
1.3切变
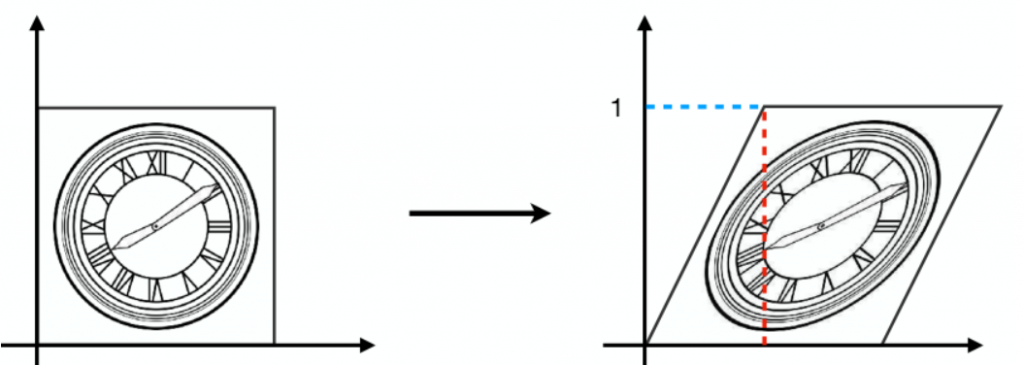
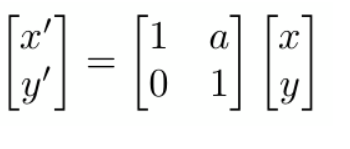
1.4旋转
注意:旋转矩阵是以原点作为基准的。
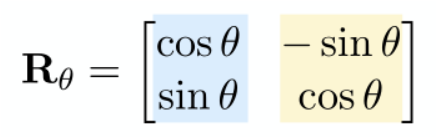
2、仿射变换与齐次坐标
以上都是图形会发生的基本变换可以总结为一个同阶矩阵*原坐标,但是当我们想要进一步平移时,问题出现了。哎?
想要实现平移,我们的运算就是X`= x+tx;
转变矩阵你就会发现,不能以之前的矩阵相乘获得,需要额外加一组列向量;
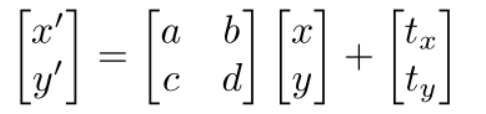
其实平移变换是非线性变换,只能用以上矩阵形式表示,叫仿射变换
但是在计算时,我们还需要额外加法运算吗?能不能和线性变换一致,统一格式。于是,齐次坐标出现了。
对于点:化为(x,y,1)T
对于向量:化为(x,y,0)T
则公式则变为:
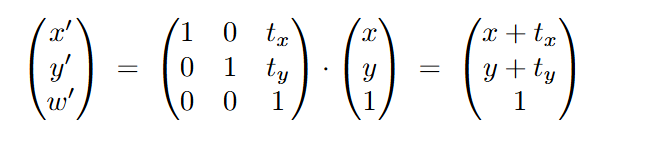
这样就实现了.
所以以上2维就需要全部变为3阶,这也是齐次坐标比原阶数多一阶的原因。

逆变换与组合变换
根据矩阵的特征,逆矩阵与矩阵相乘会变为单位矩阵,因此我们可以借助逆矩阵将经过矩阵变换的图像还原。
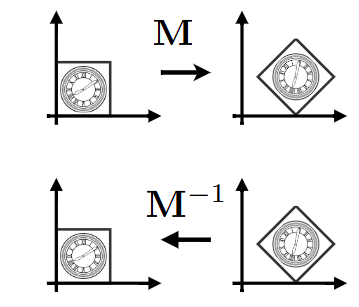
对于同一图形进行多种变换,即将不同的变换矩阵进行左乘即可,不过需要注意,如果想让物体自身旋转,需要先回复到原点位置再旋转,最后再移回去。
3D 变换
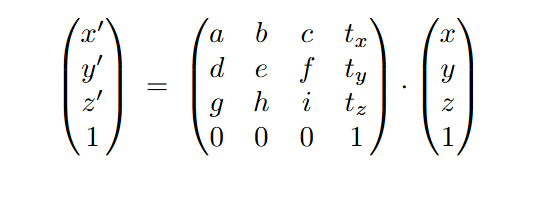


Comments | NOTHING